Copyright © 2007-2018 Russ Dewey
Depth Perception
When we look directly at an object, the image falls mostly on the fovea, a tiny portion of the retina. The brain must compute the three-dimensional structure of reality from information sent from retina to brain along the optic nerves.
In 1867 Hermann von Helmholtz described the processes of perception as unconscious inference. The brain uses cues from the environment to infer what is true of the external world. It does so unconsciously, automatically. We experience the results: 3-D perception.
Depth cues are objectively real sources of information. They are used in computer systems that model 3-D environments, such as the guidance systems of self-driving cars. Such systems must quickly construct a 3-D model of the local environment, a task similar to that of the human perceptual systems.
What is interposition as a depth cue?
Interposition is one depth cue. We (or computers) logically assume that an object cutting in front of another object is closer to us. In the figure below, the triangle looks closer than the circle, while the circle looks closer than the rectangle.
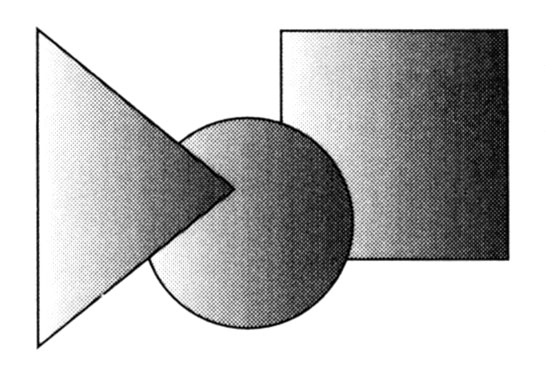
Interposition as a depth cue
Linear perspective–the tendency of parallel lines to converge in the distance–is a depth cue employed by artists since the Middle Ages. Art students are taught to draw lines to a point on the horizon, as a guide for drawing in perspective.
Most of the depth cues we will discuss are familiar to art students. They are all used by painters to suggest depth in paintings.
What is the depth cue of linear perspective?

Linear perspective as a depth cue
The road leads to a point on the horizon, creating an impression of depth that influences our interpretation of other parts of the picture. A human figure, which looks normal at a distance, appears tiny when copied to the near side of the road.
This effect illustrates the process Helmholtz called unconscious inference. We infer (logically deduce) the physical size of the figures, depending on what we "know" about their distance from us.
How does the road picture illustrate Helmholtz's concept of "unconscious inference" twice?
In this case, that knowledge is itself an inference from lines converging in the distance. The inference is reasonable, but strictly speaking it is wrong.
In reality, the picture is flat. It is not stretching into the distance, and the two figures are the same size. (If you want to get really picky, it is not even a picture, just pixels on a screen, giving enough information to form the gestalt of a road stretching into the distance.)
Binocular Disparity
Another important depth cue is binocular disparity. This is the slight difference in visual images reaching the two eyes.
A closer object produces greater binocular disparity than a distant one, as you can verify by covering first one eye then the other. Nearby objects will appear to jump as you switch from one eye to the other, showing that different images are reaching each eye. Distant objects will not appear to change position as much.
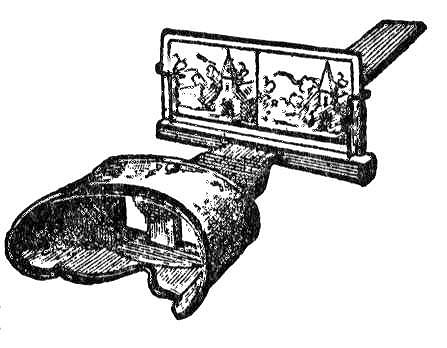
A stereoscope
Binocular disparity is responsible for the illusion of depth in stereoscopes, a favorite source of amusement in the 1800s. A stereoscope holds a card that contains two images, one visible to each eye.
Because the two images are photographed from slightly different angles, creating binocular disparity, the result is a 3-D image. In the 1800s, pictures of dramatic scenes such as the pyramids or Niagara Falls were popular.
Today the same principle is used in the Viewmaster toy familiar to many children. It is also the basis of 3-D movies, where special glasses are used to present the two eyes with slightly different images, giving an illusion of depth.
What is binocular disparity? How is it used in a stereoscope? In movies?
Barlow, Blakemore, and Pettigrew (1967) identified populations of disparity-detecting neurons that receive inputs from both eyes. They respond vigorously only if a stimulus hits the two eyes in slightly different locations. Different neurons respond to different levels of disparity, thereby providing the brain with depth information.
Motion Parallax
Relative motion of near and far objects is a cue to distance. Children discover this when looking out the window of a car.(Children may ask, "Why are the trees going by faster than the moon?")
Faraway objects appear to hold still while nearby trees, poles, and other objects zip by. This is called motion parallax.
What is motion parallax?

Motion parallax. When an observer moves, objects at different distances move at varying speeds and in different directions relative to the observer. This serves as a depth cue.
Sfumato (haze)
An additional depth cue is haze. Distant objects are more likely to be obscured by fog or haze, and their colors are somewhat purplish and washed out.
What is sfumato?
This effect is deliberately employed in the art technique called sfumato (smoke). An example is the background of the Mona Lisa. It looks hazy and far away.
Shadows
Shadows provide a depth cue. Our default assumption is that light comes from above. When shadows appear on the top of a circular pattern, this makes it look like a depression.

Shadows provide a depth cue that is reversed when the picture is turned upside-down.
When the picture is inverted (turned upside down) the shadow appears to be on the bottom of the pattern, making it look like an extruded shape or bump. In the above picture, the bowl of the plastic teaspoon on the right has shadows along its upper rim, so you can see its depth.
On the left is part of the same image (the bowl of a teaspoon) rotated 180 degrees. Now the shadow falls on the underside, creating the impression of a protruding object such as an egg.
What happens to the depth cue provided by shadows, when you turn a picture upside down?
Drawings of rectangular shapes often suggest depth by showing angular corners. We are so accustomed to seeing corners and edges of rectangular objects that we readily interpret line drawings as 3-D objects.

The impossible triangle
The impossible triangle from Penrose and Penrose (1958) is a famous example. M. C. Escher was inspired by this example and used the same principle in his spectacular artwork to portray many "impossible" situations.
The impossible triangle plays with our unconscious inference that 2-dimensional drawings represent 3-dimensional objects. Each corner appears to be a legal three-dimensional shape.
How does the impossible triangle play with our depth perception?
But the different corners do not add up to a legal gestalt. The figure is coherent on a local level (each corner by itself) but not on a global level (the figure as a whole).
Size Constancy in Visual Perception
Size constancy is the tendency of objects to keep the same apparent size even as they approach us or move farther away. Why do we not think a car is shrinking when it drives away from us, even though the retinal image is shrinking? We know it is going further away, so we take that into account.
We know this on a basic, unconscious level. We make the calculation automatically without thinking about it. That is why Helmholtz used the term unconscious inference. The visual system unconsciously infers the size of an object from cues about its distance.
Size constancy goes on all the time in visual perception. You can experience a momentary collapse of size constancy with a simple demonstration.
Hold one of your hands at arm's length, palm toward your face. Hold the other hand closer to you. Close one eye (to eliminate the depth cue of binocular disparity).
Now pretend a small child has just thrust a hand up next to yours, saying, "Look! My hand is just like yours, only smaller!"
Suddenly your hands will not look the same size. The more distant one will look closer and smaller that it really is.
Why does this happen? Using imagination you have given your visual system a reason to interpret the smaller retinal image as a small, nearby hand rather than a distant, larger hand. This shows the influence of knowledge or cognition on perception.
What is size constancy? How can you make your own hand look suddenly smaller?
The occasional failure of size constancy is a source of wonder to children. My youngest son, when he was six, exclaimed, "Hey! Buildings aren't even as big as your finger!" He was holding his finger up in front of his eye, and it dwarfed the size of distant buildings.
Psychologists explain size constancy with Emmert's Law: known distance determines apparent size. If you get strong cues that a thing is far away, you will judge it to be larger.
Moviemakers use a lack of distance cues to make you think a small object is large. In effect, they reverse Emmert's Law. If you don't know how far away a model is, you cannot determine its actual size.
Then you can assume the small model is something huge. In science fiction series, starships and space stations are models a foot or two across.
They are surrounded by a sky full of stars. There are no depth cues. Therefore the small models are readily interpreted as large objects.
How do moviemakers make you think a small model is actually a huge object?
Now it is time to leave visual perception and review the other senses. We will return to the topic of how humans interpret the visual world in Chapter 7 (Cognition) in the section on visual scene analysis.
---------------------
Reference:
Barlow, H. B., Blakemore, C., & Pettigrew, J. D. (1967) The neural mechanism of binocular depth discrimination. Journal of Physiology (London), 198, 327-342.
Write to Dr. Dewey at psywww@gmail.com.
Don't see what you need? Psych Web has over 1,000 pages, so it may be elsewhere on the site. Do a site-specific Google search using the box below.
